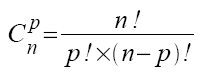1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
1 10 45 120 210 252 210 120 45 10 1
1 11 55 165 330 462 462 330 165 55 11 1
1 12 66 220 495 792 924 792 495 220 66 12 1
Les nombres ci-dessus, disposés géométriquement en triangle vous rappellent probablement quelques choses…
Ils s’agit des coefficients binomiaux que l’on obtient en développement des expressions du genre (a+b)2=1a2+2ab+1b2
Dans cet disposition géométrique chacun des nombres s’obtient en ajoutant le nombre du dessus et son voisin de gauche.
Ces nombres nous les avons déjà évoqués ici, il s’agit des C(n,p) qui servent à dénombrer le nombres de parties à p éléments d’un ensemble à n éléments.
(Par exemple on a vu dans ce billet que C(52,5)=2 598 960 nous donne le nombres de mains au poker)
On démontre aisément que C(n,p) = C (n-1,p-1) + C (n-1, p), et on peut utiliser cette formule pour se créer une fonction en Python pour calculer de façon récursive les C(n,p)
if p==0 or n==p:
return 1
exit
return cnp2(n-1,p-1)+cnp2(n-1,p)
Pour aller plus loin :
http://fr.wikipedia.org/wiki/Coefficient_binomial
Ressources :
Découvrez : une large gamme de logiciels en ligne et hors-ligne,des applications pour tablettes tactiles,
des fichiers d’exercices et des dossiers pédagogiques,les manuels scolaires et les cahiers iParcours,
des jouets multimédia pour les petits,des fichiers d’exercices pour les élèves, des applications pour iPhone et iPad,
des appareils photos, micros et accessoires audio spécialement conçus pour les enfants,des outils numériques : micros-enregistreurs et visualiseurs, etc.