Bonjour à tous,
Je vous propose cette semaine de travailler à votre rythme mais en trois étapes en suivant la progression suivante :
- Etape 1 (55 minutes)
- Etape 2 (55 minutes)
- Etape 3 (55 minutes)
Vous disposez de la possibilité de poser des questions en cliquant sur le widget « We are here! » (la page d’aide est ici !)
En cas de difficultés importantes, une connexion vidéo est envisageable !
Bon courage !
Etape 1
- https://site2wouf.fr/enclos.php (Exercice de type enclos, corrigé dans la page, j’aimerai une trace dans le cahier d’exercices)
- Vidéo à visionner
3. Leçon à mettre à jour dans le cahier (de leçons) et à apprendre :
V. Axe de symétrie d’un angle
Définition :
La bissectrice d’un angle est la demi-droite qui partage cet angle en deux angles de même mesure.
Propriété :
La bissectrice d’un angle est un axe de symétrie de cet angle
Construction :
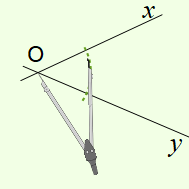
Pour tracer la bissectrice de l’angle, on trace un arc de cercle de centre O qui coupe chaque côté de l’angle en un point.
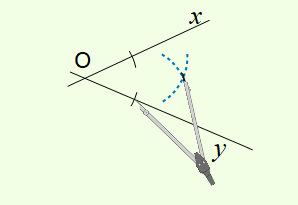
On trace deux arcs de cercle de même rayon ayant ces deux points pour centres. Ces arcs se coupent en un point.
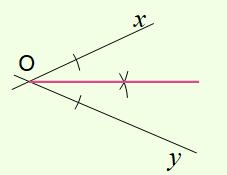
La bissectrice de l’angle est la demi-droite d’origine O passant par ce point.
Etape 2
- 1. Visionner : https://mathenpoche.sesamath.net/?page=sixieme#sixieme_3_5_7_sesabibli/4291
- 2. Leçon à mettre à jour dans le cahier (de leçons) et à apprendre :
VI. Figures usuelles et axes de symétries
Triangle isocèle
Un triangle isocèle a un axe de symétrie qui est à la fois la médiatrice de sa base et la bissectrice de son angle principal.
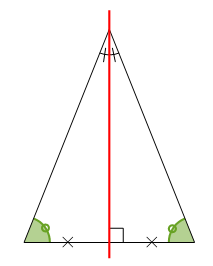
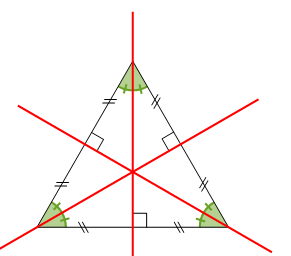
Triangle équilatéral
Un triangle équilatéral a trois axes de symétrie qui sont à la fois les médiatrices de ses côtés et les bissectrices de ses angles.
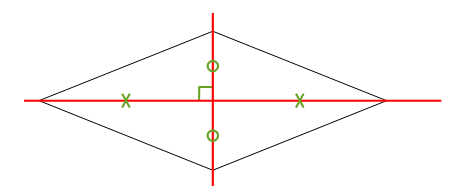
Losange
Un losange a deux axes de symétrie qui sont ses diagonales.
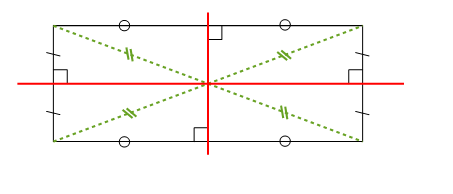
Rectangle
Un rectangle a deux axes de symétrie qui sont les médiatrices de ses côtés.
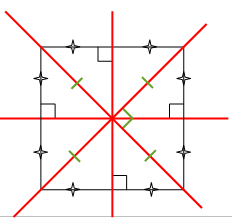
Carré
Un carré a quatre axes de symétrie qui sont les médiatrices de ses côtés et ses diagonales (un carré est à la fois un losange et un rectangle).
Etape 3
- 1. Leçon à mettre à jour dans le cahier (de leçons) et à apprendre :
VII Autres propriétés : conséquences
Dans un triangle isocèle, les angles à la base ont la même mesure.
Dans un triangle équilatéral, tous les angles ont la même mesure (60°).
Dans un losange, les diagonales se coupent en leur milieu et sont perpendiculaires.
Dans un rectangle, les diagonales se coupent en leur milieu et ont la même longueur.
Dans un carré, les diagonales se coupent en leur milieu, sont perpendiculaires et ont la même longueur.
- 2. Exercices interactifs :
https://mathenpoche.sesamath.net/?page=sixieme#sixieme_3_5_5_sesabibli/5efc7f7562855041607be854


