Rétro échecs : Les Blancs jouent et gagnent
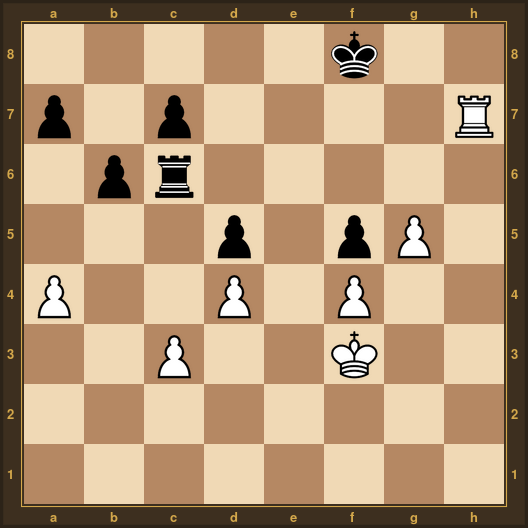
J’ai retrouvé cet exercice dans un vieux Jeux et stratégie. et j’avoue y avoir passer un peu de temps. On est loin du mat, on a le pion c3 en prise., et il faut aussi penser à …c5 derrière…. Ce…

J’ai retrouvé cet exercice dans un vieux Jeux et stratégie. et j’avoue y avoir passer un peu de temps. On est loin du mat, on a le pion c3 en prise., et il faut aussi penser à …c5 derrière…. Ce…

Si vous tenez un blog sur les échecs avec WordPress, vous connaissez peut-être déjà Chessdiag, le petit plugin qui permet d’insérer des diagrammes d’échecs directement dans vos articles grâce à un simple shortcode. Bonne nouvelle : le site chessdiag.org a…

Comment progresser aux échecs à l'ère numérique ? Découvrez un guide complet pour retrouver l'âme des pièces, choisir vos mentors et sortir de la dictature du blitz.

Le Bulletin officiel n°10 du 5 mars 2026 publie le nouveau programme de mathématiques du cycle 4 pour les classes de 5e, 4e et 3e. Que contient réellement ce texte ? Quelles évolutions introduit-il par rapport aux programmes précédents ? Voici une lecture synthétique des nouveaux textes, suivie du regard d’un enseignant après plus de trente années passées au collège.

Publié en 1980 dans Jeux & Stratégie, le jeu « saute-mouton » illustre déjà une pensée algorithmique étonnamment moderne. Cet article en propose une lecture pédagogique : logigramme, code Python, JavaScript et mise en perspective historique.

Pourquoi un problème de ponts datant de 1736 régit-il encore nos algorithmes modernes ? Découvrez l'héritage d'Euler avant de plonger dans l'enfer des graphes hamiltoniens.

Marre des problèmes de mise en page entre Word, PDF et Markdown ? Découvrez Pandoc, le "couteau suisse" gratuit qui convertit tous vos documents en un clin d'œil. Que vous soyez sous Ubuntu, Windows ou Mac, apprenez à dompter cet outil magique pour libérer vos textes et gagner un temps précieux.

En Mathématiques, “choisir” sans tenir compte de l’ordre, c’est la combinaison. En Python, c’est exactement ce que fait itertools.combinations : il énumère toutes les sélections possibles de taille k parmi une liste, sans doublon, et sans permutation inutile. Résultat :…

Il y a quelque temps, je me demandais si Xenu, ce vieux crawler bien connu des webmasters, avait encore quelque chose à dire en 2026. Verdict : oui… mais dans un cadre très précis. Rapide, rustique, efficace pour traquer les…

Janvier 2017, casino de Pittsburgh. Quatre des meilleurs joueurs de poker au monde – Dong Kim, Jason Les, Jimmy Chou et Daniel McAulay – s’installent autour d’une table pour un défi inédit : affronter Libratus, une intelligence artificielle développée par…