Article et sources mis à jour le 16/12/2018
Je ne suis pas passionné de généalogie, mais je m’intéresse à la façon de numéroter ses ancêtres (Le côté mathématique de la chose).
Ainsi à la trentième génération vous avez plus de cinq cents millions d’aïeuls !
Les généalogistes utilisent pour leur associer un code différents à chacun, la méthode SOSA :
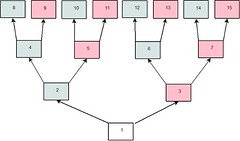
La personne dont on dresse l’ascendance porte le numéro 1.
Son père porte le numéro 2 et sa mère le numéro 3.
Ainsi on associe toujours au père le double du code de l’enfant, et à la mère le code du père augmenté de 1.
Ainsi à part la première personne qui peut-être un homme ou une femme, chaque individu de code pair est un homme et chaque individu de code impair est une femme.
Le problème c’est qu’un nombre est peu parlant. Qui est l’ancêtre numéro 54 ?
J’ai développé une petite application en Python qui nous en dit plus !
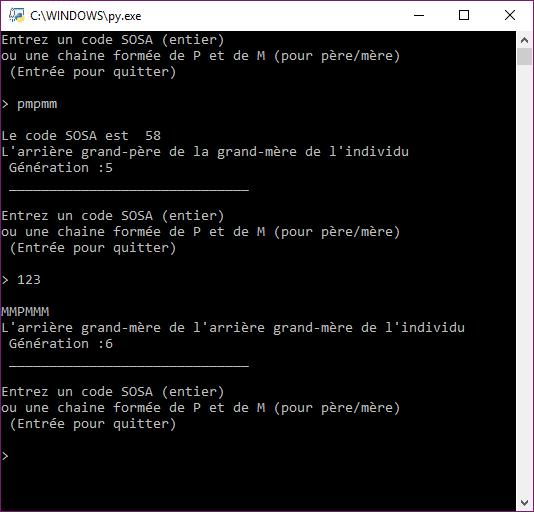
Cette application vous permet de trouver également le code SOSA du père de la mère du grand-père d’un individu :
Téléchargement :
setup.exeCe programme vous intéresse ? Voici le code :
Code Python traduit en HTML:# -*- coding: UTF-8 -*-
#Wouf 16/12/2018
# Autour du SOSA
#Fonctions principales chaine() et sosa()
def chaine(n):
""" n est un entier (code SOSA) la fonction renvoie une chaîne
formée de M et P"""
if n==1:
return ""
else:
if n%2==0:
return "P" +chaine(n//2)
else:
return "M" +chaine((n-1)//2)
def sosa(chaine):
""" renvoie le SOSA d'une chaine de la forme PPM
pour le père du père de la mère"""
code=1
for lettre in chaine[::-1]:
code*=2
if lettre=="M" :
code+=1
return code
#Fonctions entrée/sortie : ecrire() et francais()
def ecrire():
q="""Entrez un code SOSA (entier)
ou une chaine formée de P et de M (pour père/mère)
(Entrée pour quitter)
"""
print(q)
reponse=input("> " ).upper()
print()
nb=set("0123456789" )
digit=set("PM" )
if reponse=="" or reponse=="0" :
return False
elif set(reponse) <= nb:
print(chaine(int(reponse)))
print(francais(chaine(int(reponse))))
return True
elif set(reponse)<= digit:
print("Le code SOSA est " ,sosa(reponse))
print(francais(reponse))
return True
else:
return False #pour quitter l'appli
def francais(chaine):
"""Reçois une chaine genre PPMPM et la traduit en français"""
arriere_grand_parent=len(chaine)//3
reste=len(chaine)%3
grand_parent=reste//2
parent=reste%2
reponse=""
for i in range(arriere_grand_parent):
if i==0:
if chaine[0]=="P" :
reponse="L'arrière grand-père"
else:
reponse="L'arrière grand-mère"
else:
if chaine[i*3]=="P" :
reponse+=" de l'arrière grand-père"
else:
reponse+=" de l'arrière grand-mère"
for i in range(grand_parent):
if arriere_grand_parent==0 and i==0:
if chaine[0]=="P" :
reponse="Le grand-père"
else:
reponse="La grand-mère"
else:
if chaine[arriere_grand_parent*3+i*2]=="P" :
reponse+=" du grand-père"
else:
reponse+=" de la grand-mère"
for i in range(parent):
if arriere_grand_parent==0 and grand_parent==0 and i==0:
if chaine[0]=="P" :
reponse="Le père"
else:
reponse="La mère"
else:
if chaine[arriere_grand_parent*3+grand_parent*2+i]=="P" :
reponse+=" du père"
else:
reponse+=" de la mère"
if chaine=="" :
reponse="L'individu"
else:
reponse+=" de l'individu"
reponse+="\n Génération :" +str(len(chaine))+"\n ______________________________"
return reponse
#__________________________________________ le corps du prog
if ecrire():
print()
while ecrire():
print()
Bonjour,
Le nom complet de cette numérotation est « Stradonitz-Sosa ». Autre chose, ce n’est biensûr pas un but en lui même mais un simple « n° de classement » en généalogie « ascendante ».
J’ai par ex une ascendance sur plus de 52 générations, imaginez les longueurs des références qui n’entrent plus dans certains fichiers numériques du commerce.
Vous avez encore bien à apprendre ds nos systèmes comme celui d’une « généalogie descendante ».
C’est le système que j’utilise, ne me concentrant plus que sur une seule famille, mais l’étudiant en entier.
Elle nécessite un système numérique bien plus complexe car prend en compte et par individu plusieurs mariages ainsi qu’une quantité non limitée d’enfants.
J’ai notamment un cas partant de 980 si ça vous intéresse … le problème est très complexe car une même personne peut donc avoir plusieurs n° selon telle ou telle autre filiation !
En effet, les enfants d’une branche peuvent se perdre de vue, ne pas se savoir parent, et après plusieurs générations se marier entre-eux.
C’est d’ailleurs ce qui limite fortement les cas de doublons, que l’on nomme implexes : on stoppe de suite la recherche en indiquant le n° pour trouver la suite.
J’ai ainsi cessé de compter le nombre de fois qu’une seule branche était carolingienne (à 15000), et elle a une branche aînée qui en a certes bien plus encore !
Vous comprenez donc la nécessité de ce qui était dit juste au paragraphe précédent :
– sinon vous avez énormément de redondances
– et quel intérêt à recopier plus de 15000 fois l’acendance de la même personne ?
La mémoire d’un pc explose alors très vite …
J’aime aussi les maths mais il faut savoir s’en servir mais ce n’est jamais mon but primaire.
Ainsi la difficulté est, au bout d’un moment de savoir l’ordre des naissances et parfois même des mariages … surtout en certaines époques assez reculées.
Ex : Charlemagne a eu :
– bien des enfants,
– des mariages,
– des compagnes
et parfois même de très très proches au point que l’histoire cache parfois de croustillantes choses : telle l’histoire du comte de la Marche de Bretagne, Roland, mort à Ronceveaux, enterré à Blaye-Gironde … pour qui Louis le Pieux a fait modifier tous les textes pouvant tomber sous sa juridiction ; eh bien, ils ont oublié les versions finlandaises, basques et islandaises.
Toutes ont une chose en commun, donnant l’Empereur à la fois comme père et oncle.
Elles ne pouvaient pourtant du fait des langues et des distances communiquer entre elles !
Voyez-vous ce que cela signifie ?
J’arrête car vais manquer de place, pouvant vous écrire plusieurs livres …
amicalement
alba
ps : vous pouvez répondre ici et je vous inviterai à en découvrir bien plus !
Merci alba,
Votre commentaire est fort intéressant !
Je suis en train de réflechir à un système de classement basé sur… la génétique.
En gros, si deux individus ont respectivement un code A et un code B, j’aimerai que le système de codage soit capable de donner leur degré de parenté.
Mais peut-être ce système existe-t-il déjà ?
J’ai entendu il y a quelques mois qu’il existe une théorie selon laquelle il n’y avait plus que 2000 humains il y a 70 000 ans.
Je n’ai pu m’empêcher de penser au nombre astronomique d’ancêtres que nous avons à la 1000e génération.
À la 100e génération, nous avons 633 825 300 114 114 700 748 351 602 688 ancêtres. (30 chiffres)
À la 1000e génération, nous avons 5 357 543 035 931 336 604 742 125 245 300 009 052 807 024 058 527 668 037 218 751 941 851 755 255 624 680 612 465 991 894 078 479 290 637 973 364 587 765 734 125 935 726 428 461 570 217 992 288 787 349 287 401 967 283 887 412 115 492 710 537 302 531 185 570 938 977 091 076 523 237 491 790 970 633 699 383 779 582 771 973 038 531 457 285 598 238 843 271 083 830 214 915 826 312 193 418 602 834 034 688 ancêtres. (301 chiffres)
Je vous présente ces questions puisque vous semblez fort en mathématiques.
Q. 1. Théoriquement, combien une seule personne est, en moyenne, notre ancêtre il y a 70 000 ans avec cette théorie ?
Q. 2. Pour revenir à des distances temporelles plus proches, combien de générations nous séparent en moyenne de l’an 0 de notre ère ? 70 générations ? Combien de fois une seule personne est-elle, en moyenne, notre ancêtre compte tenu du nombre de personnes vivantes en l’an 0 de notre ère et sachant qu’à la 70e génération nous avons 590 295 810 358 705 651 712 ancêtre ?
Merci !