
Combien ananas a-il d’anagrammes ? Si toutes les lettres étaient différentes on répondrait sans hésiter factorielle de 6 (6!=720) mais les 3 A et les deux N nous obligent à réfléchir davantage…
Pour le doublons N (Nous avons étudier ce cas précédemment) il suffira de diviser par 2… Mais pour les 3A ?
L’erreur commune (et attendue) est la division par 3 (donc par 3 fois 2, soit par 6 pour trouver en fin de compte 120=5!)
Réfléchissons mieux 😉
Nos 3 A que l’on pourrait baptiser A1, A2 et A3 ont combien de façons de s’agencer les uns par rapports aux autres ?
- A1 A2 A3
- A1 A3 A2
- A2…
Nous avons déjà étudié ce problème c’est le nombre de permutation d’un ensemble à 3 éléments !
Il ya 3!=6 façons de permuter nos 3.
Et tout se tient ! Il y avait effectivement 2!=2 façons de permuter nos N
La réponse au problème est maintenant limpide :
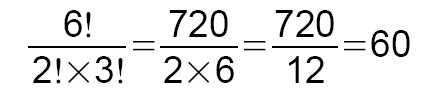
Il y a 60 anagrammes à ANANAS
Il peut arriver de douter de son raisonnement et le développement d’un petit programme en Python peut nous conforter :
2 : a a a n s n
3 : a a a n n s
4 : a a s a n n
5 : a a s n a n
6 : a a s n n a
7 : a a n a s n
8 : a a n a n s
9 : a a n s a n
10 : a a n s n a
11 : a a n n a s
12 : a a n n s a
13 : a s a a n n
14 : a s a n a n
15 : a s a n n a
16 : a s n a a n
17 : a s n a n a
18 : a s n n a a
19 : a n a a s n
20 : a n a a n s
21 : a n a s a n
22 : a n a s n a
23 : a n a n a s
24 : a n a n s a
25 : a n s a a n
26 : a n s a n a
27 : a n s n a a
28 : a n n a a s
29 : a n n a s a
30 : a n n s a a
31 : s a a a n n
32 : s a a n a n
33 : s a a n n a
34 : s a n a a n
35 : s a n a n a
36 : s a n n a a
37 : s n a a a n
38 : s n a a n a
39 : s n a n a a
40 : s n n a a a
41 : n a a a s n
42 : n a a a n s
43 : n a a s a n
44 : n a a s n a
45 : n a a n a s
46 : n a a n s a
47 : n a s a a n
48 : n a s a n a
49 : n a s n a a
50 : n a n a a s
51 : n a n a s a
52 : n a n s a a
53 : n s a a a n
54 : n s a a n a
55 : n s a n a a
56 : n s n a a a
57 : n n a a a s
58 : n n a a s a
59 : n n a s a a
60 : n n s a a a



merci!
avec le petit algo python en prime. je suis sur que ce petit exemple va m’aider dans le dev d’un correcteur / générateur de propositions pour moteur de recherche!
L’algo est loin d’être optimisé 🙂
PETKO PETKOV In my opinion in prbelom N 2 Seetharaman Kalyan demonstrates a very original and interesting complex of fairy-motives. The play of both black Lions we can define as Reciprocal Bristol on two opposite directions . Yes, this combination is very rare when it is executed with identical pieces (here=LEOs). I think that concerning all Bristol types it is not needed to speak about critical moves , despite in Bristol combination exist some critical elements . According to white play here, I doubt that everything is made optimum. White Leo stands a little bit passive on square g8 and probably it prompts what should be the white play. Аn interesting new version (but in 3 moves and without twins) is possible in which is added the new interesting and also rear motive preliminary moves by the white LEO on g8, g7 before critical moves. After that follows the author`s combination without any changes. In my opinion here we can cal white play so: White Leo`s roundabour maneuvers with critical moves and creation of anti-batteries . I show here only a position scheme which probably is possible to improve in technical aspect. See my idea at:
Que veul dire les (!)
c est la notation pour une factorielle: 5!= 5*4*3*2*1 . n! est le produit des n premiers nombres entiers.