Avant tout les courbes de Bézier appartiennent au vocabulaire mathématique :
Les courbes de Bézier sont des courbes polynomiales paramétriques décrites pour la première fois en 1962 par l’ingénieur français Pierre Bézier qui les utilisa pour concevoir des pièces d’automobiles à l’aide d’ordinateurs. Elles ont de nombreuses applications dans la synthèse d’images et le rendu de fontes. Elles ont donné naissance à de nombreux autres objets mathématiques.
L’amateur d’infographie vectorielle se doit de les maitriser, et ce billet vise à débroussailler un peu le contenu hétéroclite de la toile mondiale, afin d’en tirer les informations primordiales, substantifique moelle qui permettra à chacun de mieux les appréhender.
Nous n’évoquerons ici que les courbes de Bézier cubiques, à deux nœuds (terminaux).
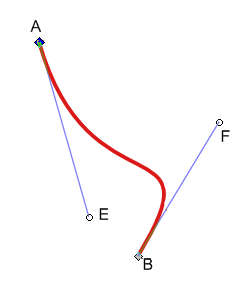
Si on plonge dans le champ lexical de l’infographie, les points A et B sont des noeuds. Ils déterminent l’origine et l’extrémité de notre première courbe de Bézier. Les points E et F sont des poignées (ou points de contrôle).
Dans inkscape, pour tracer ceci, j’ai sélectionner l’outil courbe de Bézier dans le menu (ou SHIFT F6), j’ai cliqué pour engendrer le premier point (A) et double cliqué pour terminer la courbe et créer le deuxième point (B)
J’ai ensuite sélectionné l’outil d’édition des noeuds (F2) puis cliqué sur la courbe (en maintenant le bouton appuyé) et déplacé légèrement la souris. Les poignées sont alors apparues et je les ai légérement bougé en utilisant la même technique.
Il y a quelques années, lorsque j’ai rencontré ma première courbe de Bézier, j’ai trouvé ça amusant, mais il me faut l’avouer : Je travaillais à tâtons pour parvenir à un résultat (médiocre) sans comprendre ce que je faisais…
Ce qu’il faut comprendre :
Les points E et F servent respectivement à indiquer comment la courbe part du point A, et comment elle arrive au point B. Sans parler de vecteur ou de tangente pour ne pas vous faire fuir, on peut considérer que ces points E et F sont des étapes sur un certain trajet, et que la courbe, fainéante et un peu tricheuse, donne l’illusion aux observateurs placés au départ et à l’arrivée qu’elle y passe, alors qu’elle s’évertue à couvrir la distance la plus courte possible.
C’est cette façon un peu enfantine de voir les choses qui m’a (un peu) aider à maitriser ce fabuleux outil !
Je n’ai évoqué ici que les courbes possédant deux noeuds terminaux, (un clic pour le premier, un double-clic pour le deuxième ) mais on peut construire des courbes ayant plusieurs noeuds intermédiaires.(clic,clic,et double clic pour terminer, pour une courbe de Bézier à trois noeuds). On considèrera alors que c’est une course par étape, avec les même règles!
Fort de ce que nous avons appris, le petit exercice suivant ne devrait pas poser de problème.
Dans les courbes suivantes, seules deux d’entre-elles ont plus de deux noeuds.
Lesquelles ?
(Un indice, les deux chiffres donnent alors mon département de naissance, postez simplement son chef lieu en commentaire et vous êtes mon héros)




Valence ?
Ce ne serait pas Valence par hasard ? ^^
(ou bien Arras mais bon faut savoir dans quel ordre)
Merci pour tes explications, je cherche justement le maximum de pédagogie pour apprendre à quelqu’un illustrator. 🙂
La citation d’introduction est un peu compliquée quand même, moi on me l’avais appris comme ça :
Y a un mec génial, qui s’appelle Bézier, et qui a trouvé que n’importe quelle courbe pouvait représentée par une formule mathématique.
(le prof nous fait un gribouilli au tableau avec des traits dans tout les sens)
Voilà ! Il a trouvé le moyen de représenter ça par une formule mathématique. 🙂
Du coup, le stockage est beaucoup plus léger, le redimensionnement n’est plus un problème car il suffit d’augmenter (ou diminuer) le facteur de la formule.
Ce n’est pas tout à fait exact mais ça m’était apparu tellement clair.
Bonne continuation, je vais regarder ce que tu as écrit d’autre :p
Al
La_ristourne, tu es donc mon héros !
Il s’agissait en effet d’Arras (62), la plus belle cité de l’univers… (David n’était pas loin, sauf à vol d’oiseaux)
Merci pour ton complément qui il est vrai peut éclaircir un peu les idées.
Les courbes 2 et 6 ne peuvent en effet être construites avec seulement deux noeuds terminaux :
Pour la courbe 2, on imagine bien où se situe le noeud intermédiaire : au point à l’extrême droite de la courbe la continuité de celle-ci, anguleuse, pouvez mettre la puce à l’oreille.
Pour la courbe 6 :
« la courbe, fainéante et un peu tricheuse, donne l’illusion aux observateurs placés au départ et à l’arrivée qu’elle passe sur les points de contrôle, alors qu’elle s’évertue à couvrir la distance la plus courte possible »
En réfléchissant avec cet axiome en tête, on comprend vite, que sans noeud intermédiaire, il n’y aurait jamais eu de boucle !
Bon dimanche à tous !
J’avais mal à la tête mais en vous lisant c’est pire…Bézier ? moi j’m bien Toulouse , Fabien Pelouse…
Heureusement que ça n’ est pas Poincaré qui a trouvé les courbes;-)