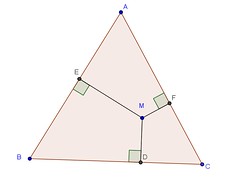
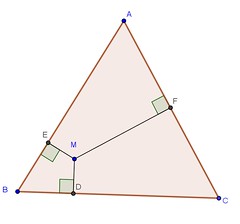
Le problème est le suivant. On a un triangle équilatéral ABC, un point M, d’humeur bucolique qui se promène dans le triangle.
On appelle D, E et F les pieds des perpendiculaires en M au trois côtés du triangle.
Question : Ou doit-on placer M pour que la somme MD+ME+MF soit minimum ?

J’aime beaucoup ce type de problème, simple mais qui parait ardu quand on ne sait pas par quel bout le prendre.
On commence tous par laisser parler son intuition.
Paroles d’élève :
– » C’est simple, on a qu’à coller M sur un sommet (Le jeune homme avait dit « coin » mais je n’ai plus l’audition excellente que j’avais à 20 ans NDLR) , on aura alors plus qu’un segment, ça sera forcement plus petit !
– « Bah non, ton trait sera vachement plus long que si on le met au milieu d’un côté ! »
– » Oui mais toi il t’en reste deux, des segment, et deux est plus grand que 1… »
– » Dans un triangle équilatéral, on sait que les intersections de toutes les droites remarquables sont au même endroit. A tous les coups c’est là ! »
-« Pas con ! »
-« Euh, avec 3 segments on aurait une distance plus courte qu’avec un seul ? je veux bien parier ! »
– » On a qu’à essayer sur l’ordi »
Oh comme elle est bonne cette idée ! Nous disposons d’outils puissants et agréable à utiliser, comme geogebra, qui peuvent nous donner la piste à suivre. On sait tous qu’il faudra démontrer quelque chose, mais avant de se lancer, ayons une conviction forte du résultat !
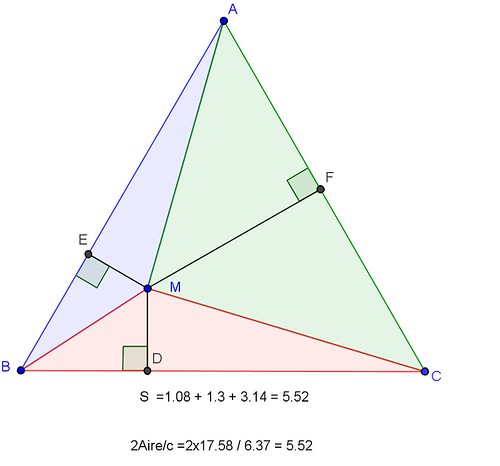
En bougeant le point M, on s’aperçoit qu’il semble bien que la somme MD+ME+MF ne dépende pas du point M… C’est fou !
Petite remarque informatique avant de passer à la démonstration : La syntaxe pour insérer une zone de texte dans géogebra en mélangeant du texte et des valeurs est particulière et dépend de la version :
Dans la dernière que j’utilise (3.1.27) si on veut afficher A + B = valeur de A + valeur de B = valeur de (A+B) on doit entrer :
» A + B = » + A + » + » + B + » = » + (A+B)Je trouve personnellement que le choix du signe « + » pour la concaténation des chaines de caractères est discutable, mais bon… Ne nous éloignons pas.

On démontre ?
On démontre
J’ai pris l’habitude de donner des indices de démonstration sous la forme d’une liste de mots, et c’est au deuxième mot que la lumière fût :
- AIRES (J’ avais souligné le S)
- PUZZLE
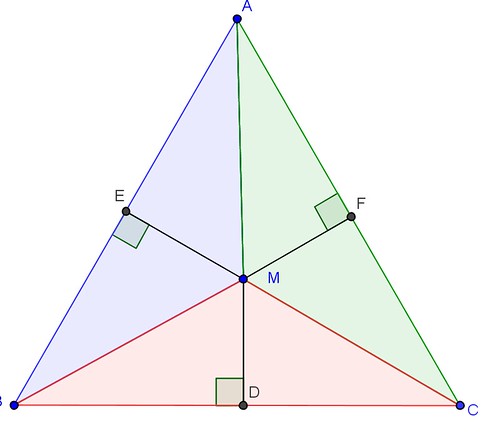
En exprimant que la sommes des aires des trois triangles de couleurs différentes est égale à A l’aire du triangle équilatéral de côté c on a :
A = MDxc/2 +MExc/2 + MF*c/2
d’où 2A= c (MD+ME+MF)
et enfin MD+ME+MF = 2A/c
Cette somme ne dépend pas de l’endroit où ce trouve M dans le triangle ABC…
Ressources :
Découvrez : une large gamme de logiciels en ligne et hors-ligne,des applications pour tablettes tactiles,
des fichiers d’exercices et des dossiers pédagogiques,les manuels scolaires et les cahiers iParcours,
des jouets multimédia pour les petits,des fichiers d’exercices pour les élèves, des applications pour iPhone et iPad,
des appareils photos, micros et accessoires audio spécialement conçus pour les enfants,des outils numériques : micros-enregistreurs et visualiseurs, etc.

non mais oh, on est dimanche aujourd’hui et tu veux nous faire bosser ? 😀
ceci dit, j’adore les maths et je regarderais ça demain 😉
bon dimanche !
Merci Wizzil, bonne semaine à toi !
et bien j’ai regardé ça et c’est à ce moment que je me suis dit , punaise les cours ça s’oublie trop vite
Moi aussi besoin de quelque heures de révision