Mathématiques pour les nuls, nombre de mains au poker

Le terme main désigne un ensemble de 5 cartes :

Par exemple:
As de trèfle, As de carreau, 8 de trèfle, 8 de pique et 6 de carreaux.

L’ordre des cartes n’a pas d’importance.

Pour bien comprendre ce billet, il peut être bon de relire:

• Factorielles (1)
• Factorielles (2)
• Factorielles (3)
• Factorielles (4)
• Factorielles (5)
• Factorielles (6)

Il y a 52 cartes dans le jeu.
Nous avons donc 52 possibilités pour la première carte. Celle-ci disparaît du jeu et il ne reste que 51 pour la deuxième, puis 50 pour la troisième, 49 pour la quatrième et enfin 48 pour la dernière.

52x51x50x49x48=311 875 200

Ce qui ne donne pas 311 875 200 mains! En effet nous avons spécifié plus haut que l’ordre n’avait pas d’importance !

photo credit: Wade From Oklahoma

Or nous avons dénombré plus de mains qu’il en a, puisqu’on a dénombré toutes les permutations possible des 5 cartes.
or il y a 5!=120 permutations dans un ensemble à 5 éléments.

La réponse au problème est donc
52x51x50x49x48/120=2598960Il y a exactement 2 598 960 mains au poker.
(On peut retenir, ça impressionne toujours en société qu’il y a environ 2,6 millions de mains au poker et que la probabilité d’avoir le plus gros jeu, soit la quinte flush royale à pique servie, est d’environ une chance sur 2,6 millions. Nous reparlerons de probabilité plus tard ! )

Qu’avons nous, mathématiquement, calculer ?

Combinaison, une définition simple :

On appelle combinaison de p élément d’un ensemble à n éléments une partie de cet ensemble ayant p éléments.

On note C(n,p) le nombre de ces combinaisons et on a:

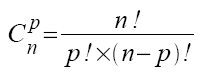
Le script Python, avec la fonction cnp(n,p) qui permet de calculer le nombres de combinaisons :

def fact (n):
    """retourne la factorielle de n""" 
    if n==0  :
        return 1
    else:
        return n*fact(n-1) #fonction récursive

def cnp (n,p):
    """retourne le nombre de combinaisons, p parmis n""" 

    if p>n:
        return "erreur" 
    result=1
    for i in range(n,n-p,-1):
        result *= i
    return result//fact(p)
def fact (n):
    """retourne la factorielle de n""" 
    if n==0  :
        return 1
    else:
        return n*fact(n-1) #fonction récursive

def cnp (n,p):
    """retourne le nombre de combinaisons, p parmis n""" 

    if p>n:
        return "erreur" 
    result=1
    for i in range(n,n-p,-1):
        result *= i
    return result//fact(p)

cnp

et un screenshot de l’IDLE: