• Un cahier proposé par des élèves

J’ai adoré l’initiative et l’originalité du travail proposé par des élèves du collège Louise Michel durant l’année 2019-2020 : Un cahier de problème et d’énigmes.

Même si au départ j’ai été choqué que ce document soit publié avec une erreur dès l’énigme 2, j’ai pris beaucoup de plaisir à le parcourir et à faire travailler des élèves de sixièmes sur ces jolis problèmes.

Parlons en premier de l’erreur évoquée, intéressante, avec en tête cette citation de John Fitzgerald Kennedy

“Une erreur ne devient une faute que si l’on refuse de la corriger.”

L’énigme 2 (Thais)

Je suis un nombre décimal compris entre 0 et 30.
Mon chiffre des dizaines est le quart de mon chiffre des unités qui est égal à 8.
Mon chiffre des dixièmes est le seul chiffre présent dans le résultat de 33÷3.
Mon nombre de millièmes est le double de 5×9 + 7.

On arrive facilement à un nombre de la forme 28,1?????? à l’aide des 3 premiers indices.

Le dernier indice nous apprends que le nombre de millièmes est 104 donc que le nombre est de la forme 0,104?????

Thais attendait surement 28,104 mais dans ce nombre il y a, hélas, 28104 millièmes ! (Si vous n’êtes pas convaincus, demandez-vous combien il y a de centimes dans 1,20€… 120 ou 20?) On aurait pu corriger le dernier indice ainsi:

Le nombre de millièmes de ma partie décimale est le double de 5×9 + 7.

L’énigme 10 : L’ascenseur étrange (Léo B)

Dans cet immeuble de onze étages, l’ascenseur est bien étrange.
Il ne peut monter que 2, 3 ou 5 étages à la fois et ne peut descendre que 4 ou 11 étages.
Le concierge, dont la loge est située au rez-de-chaussée, doit procéder à la distribution du courrier.
Comment doit-il opérer pour partir de sa loge, s’arrêter une fois et une seule à chaque étage, et revenir chez lui ?

Cet exercice est classique et amusant. Mais souvent on ne propose que 3 déplacements possibles. Et je me suis posé une question : A-t-on encore des solutions quand on ne s’autorise que 3 déplacements (Par exemple : +2, +3 et -4)

Ma contribution : une application Python 3

class Immeuble:
    def __init__(self,etages,possibles,depart=0):
        self.etages=etages
        self.possibles=possibles
        self.depart=depart

class Voyage:
    def __init__(self,passe,i):
        self.passe=passe
        self.i=i
        
    def enfants(self):
        boutons=[]
        if len(self.passe)==0:
            self.passe=[self.i.depart]
        for j in self.i.possibles:
            if  self.passe[-1]+j in [x for x in self.i.etages if x not in self.passe]:
                boutons.append(j)
        liste=[]
        
        for j in boutons :
            newpasse=[x for x in self.passe]
            newpasse.append(self.passe[-1]+j)
            liste.append(newpasse)
          
        return [Voyage(l,self.i) for l in liste]


    


def etudie(x,y,z,t=None):
    if t==None:
        t=x
    i=Immeuble(x,y,z)
    v=Voyage([],i)
    n=2
    liste=[Voyage(x.passe,i) for x in v.enfants()]
    oldliste=liste
    while len(liste) !=0:
        n+=1
       
        newliste=[]
        for k in liste:
            for l in k.enfants():
                newliste.append(Voyage(l.passe,i))
        oldliste=liste
        liste=[x for x in newliste]
       

    return [u for u in oldliste if u.passe[-1] in t]
       
        
a=etudie(list(range(12)),[2,3,5,-4,-11],0,[4,11])
compteur=0

for i in a :
    compteur+=1
    j="-".join([str(x) for x in i.passe])
    print("{}/ {}".format(compteur,j))

k=input(" FIN ")


                

Résultats :

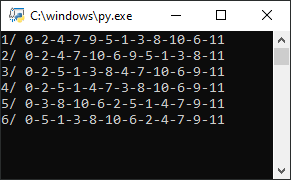
Ce qui est raccord avec la correction proposée :

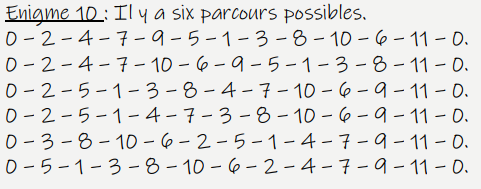
Quelques mots sur l’application Python 3

def etudie(x,y,z,t=None) est la fonction qui retourne une liste contenant les chemins.

Elle reçoit en paramètres :

• x : la liste des étages de l’immeuble ([0,1,2,3,4,5,6,7,8,9,10,11] ici)
• y: la liste des boutons ([+2,+3,5,-4,-11] ici)
• z: l’étage de départ (0 ici)
• t: la liste optionnelle des dernières étapes (ici [4,11] , les seuls permettant de rejoindre la loge au coup suivant)

Les chemins retournés dans la liste ont chacun un paramètre .passe (passé) qui est une liste des étages parcourus.

Modifions la ligne a=etudie(list(range(12)),[+2,+3,5,-4,-11],0,[4,11]) en a=etudie(list(range(12)),[+3,5,-4,-11],0,[4,11]) pour signifier que l’on a, comme choix que:

• monter de 3
• monter de 5
• descendre de 4
• descendre de 11

Nous n’avons pas de solution !

Modifions maintenant la ligne a=etudie(list(range(12)),[+2,+3,5,-4,-11],0,[4,11]) en a=etudie(list(range(12)),[+2,+3,-4,-11],0,[4,11]) pour signifier que l’on a, comme choix que:

• monter de 2
• monter de 3
• descendre de 4
• descendre de 11

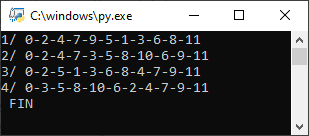
Il nous restait 4 solutions, mais seulement de 11 étapes (pas 12) . Ainsi la ligne 1 ne contient pas 10, la 2 ne contient pas 1…

Remarque :

Pour éviter ce souci, j’ai modifier le code source pour ne renvoyer les chemins que quand toutes les étapes sont parcourues :

class Immeuble:
    def __init__(self,etages,possibles,depart=0):
        self.etages=etages
        self.possibles=possibles
        self.depart=depart

class Voyage:
    def __init__(self,passe,i):
        self.passe=passe
        self.i=i
        
    def enfants(self):
        boutons=[]
        if len(self.passe)==0:
            self.passe=[self.i.depart]
        for j in self.i.possibles:
            if  self.passe[-1]+j in [x for x in self.i.etages if x not in self.passe]:
                boutons.append(j)
        liste=[]
        
        for j in boutons :
            newpasse=[x for x in self.passe]
            newpasse.append(self.passe[-1]+j)
            liste.append(newpasse)
          
        return [Voyage(l,self.i) for l in liste]


    


def etudie(x,y,z,t=None):
    if t==None:
        t=x
    i=Immeuble(x,y,z)
    v=Voyage([],i)
    n=2
    liste=[Voyage(x.passe,i) for x in v.enfants()]
    oldliste=liste
    while len(liste) !=0:
        n+=1
       
        newliste=[]
        for k in liste:
            for l in k.enfants():
                newliste.append(Voyage(l.passe,i))
        oldliste=liste
        liste=[x for x in newliste]
       
    nb_etapes=len(oldliste[0].passe)
    if nb_etapes==len(x):
    
        return [u for u in oldliste if u.passe[-1] in t]
    else:
        return []
        
a=etudie(list(range(12)),[+2,3,-4,-11],0)
compteur=0

for i in a :
    compteur+=1
    j="-".join([str(x) for x in i.passe])
    print("{}/ {}".format(compteur,j))

k=input(" FIN ")

                

Ainsi avec comme point de départ une activité proposée par un élève de sixième, de nombreuses portes se sont ouvertes, et j’ai continué un long moment à m’amuser avec cet ascenseur !

Finalement j’ai intégré au site de Wouf ces « exercices du jour » : L’ascenseur fou fou fou où je propose en téléchargement 400 problèmes gratuits en pdf de ce type.