Les Mathématiques sont une passion et mon métier. Il m’arrive d’en parler à des personnes étrangères à leur magie et étrangement, souvent elles sont captivées.
Pourtant la majorité d’entre elles souffrait (silencieusement) d’ennui en cours de Math, pendant leur scolarité.
Faire partager sa passion est un privilège, et j’ai décidé d’aborder de temps en temps des problématiques mathématiques ici en espérant simplement vous donner du plaisir ou vous réconcilier avec la beauté des mathématiques.
Certes beaucoup n’en verront pas l’utilité… Mais les implications dans la vie sans nombreuses (jeux, bricolage… ) et la mode n’est-elle pas un peu au « brain-training? »
Commençons par un problème simple :
Je dispose de 3 lettres A, B, et C pour écrire des mots de 3 lettres différentes (Sans répéter la même lettre)
Le mot « mots » désignant des suites de 3 lettres mais qui ne veulent bien entendu rien dire!
- ABC
- ACB
- BAC
- et…
Ce problème est simple car il est aisé d’écrire tous ces mots, en ayant un peu de méthode (en pourrait parler d’algorithme)
Pour ne pas en oublier, il suffit de les écrire dans un certain ordre (ABC par exemple) et d’essayer de modifier ce mot en ne touchant qu’à la lettre la plus à droite possible et en la remplaçant par la suivante dans l’ordre ABC :
- ABC
- ACB
- BAC
- BCA
- CAB
- CBA
Nous avons la réponse au problème, il y a 6 mots possibles.
Compliquons !
Je dispose maintenant de 5 lettres ABCDE, et je me pose la même question, combien de mots de 5 lettres différentes puis-je construire ?
La même technique fonctionne encore, mais elle devient laborieuse. Passons en mode « analyse » :
Nous avons évidemment 5 possibilités pour la première lettre (A, B, C, D ou E)
Si nous choisissons A comme première lettre il reste 4 possibilités (B, C, D, E) comme deuxième lettre.
Si nous choisissons B comme première lettre il reste 4 possibilités (A, C, D, E) comme deuxième lettre.
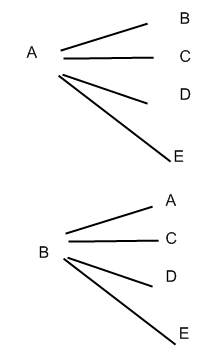
Comptons les branches de cet arbuste naissant :
Il y en a 5×4=20.
Mais l’arbre continue de grandir et à l’étape suivante chaque bourgeon va donner 3 branches :
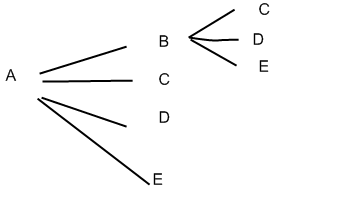
Comptons les branches de cet arbuste adolescent :
Il y en a 5x4x3=60.
A l’étape suivant deux branches apparaîtront sur chaque bourgeons et il y aura :
5x4x3x2 = 120 branches.
La dernière étape est un peu spéciale, puisqu’il ne reste qu’une lettre à ajouter au bout de chaque « branche », et le nombre de branches ne changera pas. (On peut considérer qu’on multiplie par 1)
Conclusion :
Le nombre de mots de 5 lettres différentes est 5x4x3x2x1= 120.
Ce nombre est noté 5! (5 suivi d’un point d’exclamation) et se lit 5 factorielle.
Prolongement informatique
La fonction factorielle est souvent donnée en exemple de programmation récursive : Une fonction récursive est une fonction qui s’appelle elle-même.
En effet si on a calculé 5! = 120 et que l’on veut calculer 6!
On a 6! = 6x5x4x3x2x1 = 6 x 5! =6 x 120 = 720
En javascript cela donnerait :
{
if (n<0) {
return « ### Erreur de domaine ### »;
}
else {
if (n == 0) {
return 1;
}
else {
return n * factorielle (n-1);
}
}
}
Quand on appelle factorielle(n) la fonction renvoie n x factorielle(n-1), elle doit donc s’appeler elle-même jusqu’à appeler factorielle 0 qui est 1 par convention.
- A noter que si vous entrez autre chose qu’un nombre la fonction factorielle() s’appelle ad vitam aeternam et le javascript plante.
je ne comprent pas quand vous dit que la fonction s’appelle elle meme???
merci de votre reponce
pour plus de clarté je vais noter f(n)=n! factoriel n:
On a f(n+1)=f(n)*(n+1)
Ainsi pour calculer un terme on utilise le terme précédent. Notre programme en javascript utilise cette particularité. La fonction s’appelle elle même…
je ne suis pas satisfait.
Pourquoi frank kack?
Factorielle N, Avec cette application, vous pouvez calculer la factorielle d’un nombre quelconque
https://play.google.com/store/apps/details?id=com.fjapps.juank.factorial&hl=fr