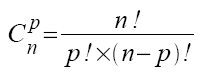Le terme main désigne un ensemble de 5 cartes :
Par exemple:
As de trèfle, As de carreau, 8 de trèfle, 8 de pique et 6 de carreaux.
L’ordre des cartes n’a pas d’importance.
Pour bien comprendre ce billet, il peut être bon de relire:
Il y a 52 cartes dans le jeu.
Nous avons donc 52 possibilités pour la première carte. Celle-ci disparaît du jeu et il ne reste que 51 pour la deuxième, puis 50 pour la troisième, 49 pour la quatrième et enfin 48 pour la dernière.
52x51x50x49x48=311 875 200
Ce qui ne donne pas 311 875 200 mains! En effet nous avons spécifié plus haut que l’ordre n’avait pas d’importance !
photo credit: Wade From Oklahoma
Or nous avons dénombré plus de mains qu’il en a, puisqu’on a dénombré toutes les permutations possible des 5 cartes.
or il y a 5!=120 permutations dans un ensemble à 5 éléments.
La réponse au problème est donc
52x51x50x49x48/120=2598960Il y a exactement 2 598 960 mains au poker.
(On peut retenir, ça impressionne toujours en société qu’il y a environ 2,6 millions de mains au poker et que la probabilité d’avoir le plus gros jeu, soit la quinte flush royale à pique servie, est d’environ une chance sur 2,6 millions. Nous reparlerons de probabilité plus tard ! )
Qu’avons nous, mathématiquement, calculer ?
Combinaison, une définition simple :
On appelle combinaison de p élément d’un ensemble à n éléments une partie de cet ensemble ayant p éléments.
On note C(n,p) le nombre de ces combinaisons et on a:
Le script Python, avec la fonction cnp(n,p) qui permet de calculer le nombres de combinaisons :
Code Python traduit en HTML:def fact (n):
"""retourne la factorielle de n"""
if n==0 :
return 1
else:
return n*fact(n-1) #fonction récursive
def cnp (n,p):
"""retourne le nombre de combinaisons, p parmis n"""
if p>n:
return "erreur"
result=1
for i in range(n,n-p,-1):
result *= i
return result//fact(p)
def fact (n):
"""retourne la factorielle de n"""
if n==0 :
return 1
else:
return n*fact(n-1) #fonction récursive
def cnp (n,p):
"""retourne le nombre de combinaisons, p parmis n"""
if p>n:
return "erreur"
result=1
for i in range(n,n-p,-1):
result *= i
return result//fact(p)
cnp
et un screenshot de l’IDLE:

Ressources :
Découvrez : une large gamme de logiciels en ligne et hors-ligne,des applications pour tablettes tactiles,
des fichiers d’exercices et des dossiers pédagogiques,les manuels scolaires et les cahiers iParcours,
des jouets multimédia pour les petits,des fichiers d’exercices pour les élèves, des applications pour iPhone et iPad,
des appareils photos, micros et accessoires audio spécialement conçus pour les enfants,des outils numériques : micros-enregistreurs et visualiseurs, etc.