Article en référence à : https://site2wouf.fr/ampoules.php

Arithmétique à l’école et au lycée : Focus sur les Multiples et les Diviseurs

L’arithmétique constitue un volet essentiel de l’enseignement mathématique, tant à l’école primaire qu’au lycée. Comprendre les multiples et les diviseurs est crucial pour développer une solide base en mathématiques. Dans cet article, nous explorerons le programme d’arithmétique tel qu’il est défini par les instructions officielles du Ministère de l’Éducation Nationale, en mettant particulièrement l’accent sur les multiples et les diviseurs.

Programme d’Arithmétique à l’École Primaire et au collège

Selon les instructions officielles du Bulletin Officiel de l’Éducation Nationale, le programme d’arithmétique à l’école primaire comprend plusieurs axes, dont :

1. Les Nombres Entiers : Apprentissage des nombres jusqu’à plusieurs centaines, compréhension de la numération décimale.
2. Les Opérations : Addition, soustraction, multiplication, division.
3. Les Fractions : Introduction aux fractions simples.
4. Les Nombres Décimaux : Notamment la connaissance des dixièmes et des centièmes.
5. Les Grandeurs et Mesures : Longueurs, masses, volumes, temps, argent.
6. Les Problèmes : Résolution de problèmes à partir des différents concepts abordés.

Dans le cadre de l’arithmétique, l’étude des multiples et des diviseurs est introduite dès les premières années de l’école primaire. Les élèves apprennent à reconnaître les multiples et les diviseurs des nombres entiers.

Multiples et Diviseurs au Collège

Au collège, le programme d’arithmétique se complexifie. Les élèves approfondissent leur compréhension des multiples et des diviseurs, et apprennent à les manipuler de manière plus avancée. Le Bulletin Officiel de l’Éducation Nationale précise que les élèves doivent être capables de :

• Identifier les multiples et les diviseurs d’un nombre.
• Utiliser les propriétés des multiples et des diviseurs dans des calculs mathématiques.
• Résoudre des problèmes impliquant les multiples et les diviseurs.

En outre, les élèves sont amenés à explorer des concepts liés tels que les nombres premiers, le PGCD (Plus Grand Commun Diviseur) et le PPCM (Plus Petit Commun Multiple).

Programme d’Arithmétique au Lycée

Au lycée, l’enseignement de l’arithmétique prend une dimension plus abstraite. Les élèves sont confrontés à des concepts plus avancés tels que les congruences, les groupes, les anneaux, et d’autres structures algébriques. Cependant, les multiples et les diviseurs restent des concepts fondamentaux qui continuent d’être explorés dans le cadre de la théorie des nombres.

Le Bulletin Officiel de l’Éducation Nationale énonce que le programme d’arithmétique au lycée vise à :

• Approfondir la compréhension des propriétés des multiples et des diviseurs.
• Utiliser les multiples et les diviseurs dans des contextes mathématiques avancés.
• Explorer les théories liées aux nombres premiers, aux congruences, et aux autres structures algébriques.

Les multiples et les diviseurs sont des concepts fondamentaux en mathématiques, qui sont introduits dès les premières années de l’école primaire et qui continuent d’être explorés tout au long du cursus scolaire. En comprenant ces concepts, les élèves développent des compétences mathématiques essentielles qui leur seront utiles dans de nombreuses disciplines. Le programme d’arithmétique, tel que défini par les instructions officielles du Ministère de l’Éducation Nationale, offre une progression cohérente pour l’étude des multiples et des diviseurs, contribuant ainsi à la formation mathématique des élèves à tous les niveaux.

Intérêt des activités ludiques

Les activités ludiques sont extrêmement bénéfiques lors de l’enseignement de l’arithmétique car elles permettent d’engager les élèves de manière interactive et stimulante. Voici quelques-uns des avantages spécifiques des activités ludiques sur ce sujet :

1. Engagement accru : Les activités ludiques rendent l’apprentissage des multiples et des diviseurs plus attractif et amusant pour les élèves. Cela les encourage à s’impliquer activement dans leur apprentissage, ce qui peut renforcer leur motivation et leur intérêt pour les mathématiques.
2. Compréhension conceptuelle : Les activités ludiques permettent aux élèves de manipuler concrètement les concepts de multiples et de diviseurs. En travaillant avec des manipulations ou en participant à des jeux, les élèves peuvent développer une compréhension plus approfondie de ces concepts, ce qui peut faciliter leur apprentissage et leur rétention à long terme.
3. Renforcement des compétences : Les activités ludiques offrent aux élèves de nombreuses occasions de pratiquer l’identification des multiples et des diviseurs, ainsi que leur utilisation dans des contextes variés. En jouant à des jeux de cartes, à des jeux de société ou en participant à des défis mathématiques, les élèves peuvent renforcer leurs compétences de manière efficace et plaisante.
4. Collaboration et communication : De nombreuses activités ludiques impliquent la collaboration entre les élèves et encouragent la communication mathématique. Travailler en équipe pour résoudre des problèmes ou jouer à des jeux peut aider les élèves à développer leurs compétences sociales tout en renforçant leur compréhension des multiples et des diviseurs.
5. Différenciation : Les activités ludiques peuvent être facilement adaptées pour répondre aux besoins individuels des élèves. Les enseignants peuvent proposer une variété d’activités avec différents niveaux de complexité, ce qui permet aux élèves de travailler à leur propre rythme et de relever des défis appropriés à leur niveau de compétence.

Les 12 ampoules

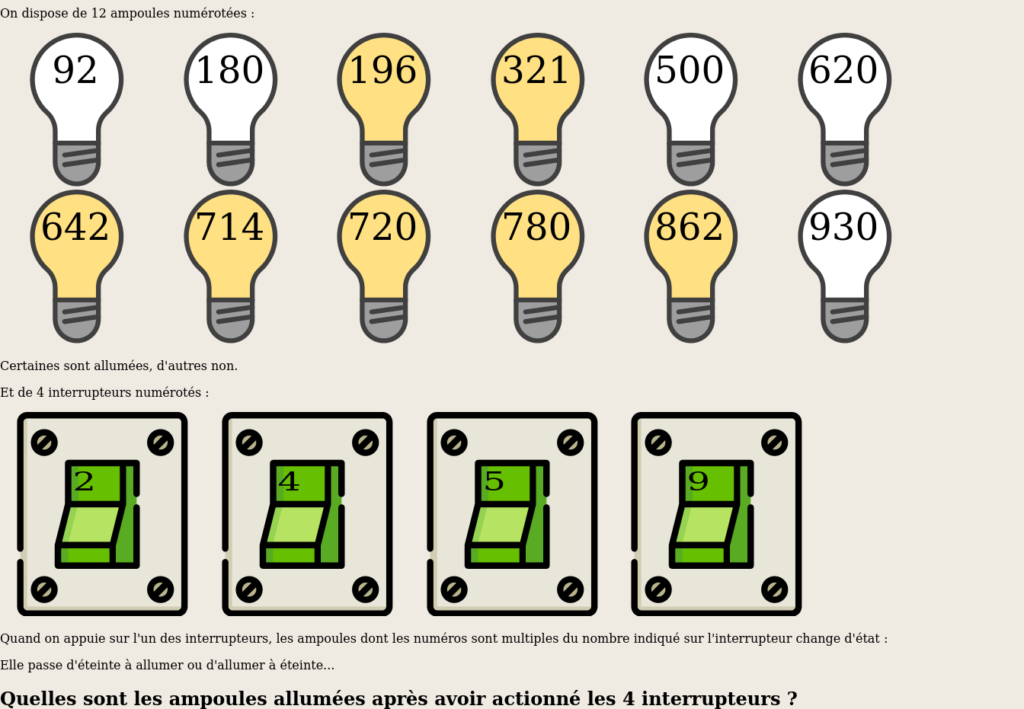
Avec cette activité on travaille sur les critères de divisibilités mais aussi sur la méthodologie devant un problème complexe : Il faut trouver une Stratégie. Par exemple on peut s’intéresser pour chaque ampoule à la parité du nombre d’interrupteurs déclencheurs…

Chaque jour sur le site2wouf.fr est affiché une activité de ce type et 400 PDF, avec les corrections, sont proposés en téléchargement gratuit.

Au niveau du code

La partie HTML des pages PHP est développée en Python3. Le code est disponible sur demande.

Au niveau des paramètres invariants, pour avoir un intérêt constant, j’ai décidé que:

• Une seule ampoule ne matchait avec aucun interrupteur
• Trois ampoules matchaient avec un seul interrupteur
• Trois ampoules matchaient avec deux interrupteurs
• Trois ampoules matchaient avec trois interrupteurs
• Deux ampoules matchaient avec tous les interrupteurs

Les numéros des ampoules sont compris entre 0 et 999

Les interrupteurs sont 4 nombres parmi :

• 2
• 3
• 4
• 5
• 6
• 9
• 10

N’hésitez pas à réagir en commentaire !