Une énigme du Monde
Un homme a marché cinq heures. D’abord sur une route plate, puis en montant une colline. Une fois en haut, il a fait demi-tour et est revenu à son point de départ par le même itinéraire. Il marche à la…
Catégorie Quotidien
Quotidien : Ce qui se passe ici et ailleurs, aujourd’hui.
Blog pourquoi et comment annoncer ses billets à l’avance.
Pourquoi annoncer ses billets à l’avance ? L’annonce anticipée de vos billets de blog est une pratique souvent sous-estimée, mais qui peut avoir un impact significatif sur votre blog. Voici quelques raisons pour lesquelles vous devriez envisager de le faire…
Pseudo.py un petit utilitaire pour créer des pseudos
La problématique était la suivante : L’équipe pédagogiques du collège dans lequel j’exerce désirait, dans le cadre de la semaine des Mathématiques, créer une activité en ligne à destination de toutes les classes de sixième. Or chaque élève joue pour…
Le Réseau Canopé, qu’est-ce que c’est ?
Le Réseau Canopé est une institution publique française créée en 1981, qui a pour objectif de soutenir les professionnels de l’éducation dans l’exercice de leur mission. Cette institution est dédiée à la production, la diffusion et l’utilisation de ressources pédagogiques…
Que voyez-vous en premier ?
En survolant un article du demotivateur ce matin je suis tombé sur cette image : Dans son article, Albane P nous apprend que si vous voyez : Deux profils : vous êtes du genre à faire facilement l’autruche et préférez généralement…
Les pièges du net : piecesauto24.com. Ou acheter ses pièces auto sur le net?
Ceux qui me connaissent savent ma passion pour les voitures anciennes. Je ne parle pas de voitures de collection mais de véhicules d’un âge certain, disposant d’un capital sympathie, et qui ne méritent absolument pas de terminer prématurément à la…
Etat des lieux du site2wouf.fr, été 2021.
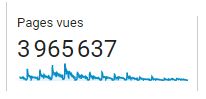
Je profite des vacances et de la météo désastreuse dans le Pas-de-Calais en ce mois de juillet pour dresser un état des lieux du site. La première version date des débuts d’internet mais la version actuelle, avec ce nom de…
Miniature : Partie viennoise (6)
Le jeu de 52 cartes
Avant propos Pourquoi, cet article ? Simplement pour avoir un support pour expliquer aux élèves qui ne connaissent pas, ce qu’est un jeu de 52 cartes. Il est vrai qu’il y a 30 ans chacun avait manipulé des cartes à…
Expression surannée : « Tintin, les haricots verts! »
Je suis né en 1967. Toute ma vie j’ai entendu de nouvelles expressions sans y prêter une attention particulière. « Tiens, on dit ça maintenant ! » me dis-je parfois, en souriant. En groupe on se pose même parfois la question…